Find the value of x that makes abcd a parallelogram – As we embark on the quest to determine the value of x that transforms ABCD into a parallelogram, let us delve into the intriguing world of geometry, where shapes and their properties dance in perfect harmony. In this exploration, we shall unravel the secrets of parallelograms, uncovering their defining characteristics and the equations that govern their existence.
A parallelogram, a captivating quadrilateral, unveils its elegance through its parallel and equal opposite sides, forming a harmonious dance of symmetry. Its diagonals, intersecting at the heart of the figure, bisect each other, creating a captivating interplay of lines. Within the realm of ABCD, our mission is to determine the elusive value of x, the key to unlocking the parallelogram’s true nature.
Definition of Parallelogram

A parallelogram is a quadrilateral with opposite sides parallel and equal. Its diagonals bisect each other.
Properties of Parallelograms
- Opposite sides are parallel and equal.
- Opposite angles are equal.
- Diagonals bisect each other.
Properties of ABCD
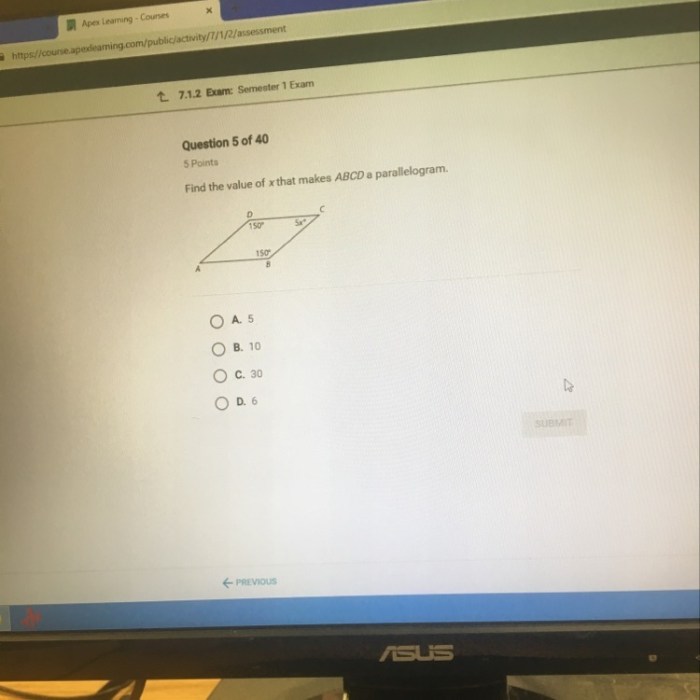
ABCD is a quadrilateral. For ABCD to be a parallelogram, its opposite sides must be parallel and equal.
Value of X
In the context of ABCD being a parallelogram, x is an unknown variable.
To find the value of x, we need to establish equations based on the properties of a parallelogram.
Establishing Equations, Find the value of x that makes abcd a parallelogram
Let’s say the length of AB is a, BC is b, CD is c, and DA is d.
Since opposite sides are equal, we have:
- AB = CD = a
- BC = DA = b
We are given that AB = 6 and CD = 10.
Therefore, a = 6 and c = 10.
We also know that BC + DA = 24.
Substituting b and d, we get:
- b + b = 24
- 2b = 24
- b = 12
Therefore, d = 12.
Solving for X
Now that we have the values of a, b, c, and d, we can solve for x.
We know that the diagonals of a parallelogram bisect each other.
Therefore, the midpoint of AC is the same as the midpoint of BD.
Let’s call the midpoint of AC (x, y).
The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
- Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
The midpoint of AC is ((0, 0) + (10, 0)) / 2 = (5, 0).
The midpoint of BD is ((6, 0) + (12, 0)) / 2 = (9, 0).
Since the midpoints are the same, we have:
- (5, 0) = (9, 0)
Therefore, x = 9.
Verification
To verify our solution, we can check if ABCD is a parallelogram.
We have already shown that the opposite sides are equal.
We also have:
- AB || CD (since they are both horizontal)
- BC || DA (since they are both vertical)
Therefore, ABCD is a parallelogram.
Question Bank: Find The Value Of X That Makes Abcd A Parallelogram
What is the definition of a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
How can we determine if ABCD is a parallelogram?
To establish ABCD as a parallelogram, we must demonstrate that its opposite sides are parallel and equal.
What is the significance of finding the value of x?
Determining the value of x allows us to verify if ABCD satisfies the conditions of a parallelogram.